algs4-1.4.12: 基于 GPT4 的思路, 进一步扩展, 尝试找出三个有序数组的公共元素

1.4.12 编写一个程序，有序打印给定的两个有序数组(含有N个int值)中的所有公共元素，程序在最坏情况下所需的运行时间应该和N成比。

TO GPT: 我的答案, 是否符合要求?

基于 “时间复杂度” 的考虑, 是我想到这个基础解答方法的关键因素:

N个元素的数组遍历, 时间复杂度必然是O(N).
如果要想保证算法复杂度依然是O(N), 那就必须保证进行 常数次 的数组遍历.

我的初版代码如下:

public class Answer1412 {
    public static void printCommon(int[] a, int[] b) {
        int N = a.length;
        if (N < 1 || N != b.length) {
            return;
        }

        int cur_a = a[0];
        int cur_b = a[0];
        if (cur_a == cur_b) {
            StdOut.println(cur_a);
        }

        int i_a = 1;
        int i_b = 1;

        // 基本策略, 数组a和b,交叉遍历. 这样,最大执行次数是 2N. 时间复杂度依然是O(N).
        for (; i_a < N && i_b < N;) {
            for (; i_a < a.length; i_a++) {
                if (cur_a == a[i_a]) {
                    continue;
                }

                cur_a = a[i_a];

                if (cur_a == cur_b) {
                    StdOut.println(cur_a);
                } else if (cur_a > cur_b) {
                    break;
                }
            }

            for (; i_b < b.length; i_b++) {
                if (cur_b == b[i_b]) {
                    continue;
                }

                cur_b = b[i_b];

                if (cur_a == cur_b) {
                    StdOut.println(cur_a);
                } else if (cur_b > cur_a) {
                    break;
                }
            }
        }
    }

    public static void main(String[] args) {
        int[] a = { 1, 2, 2, 2, 3, 4, 5, 6 };
        int[] b = { 1, 2, 3, 6, 6, 6, 7, 8 };

        printCommon(a, b);
    }
}

GPT 的回答总结:

时间复杂度确实是 O(N), 符合要求.
GPT 找到了我未曾察觉的初始化错误:

int cur_b = a[0];

GPT 给出了一个更简洁的版本, 基于 “双指针法”. 我修当修改后, 如下:

package algs4;

public class Answer1412Gpt {
    public static void printCommon(int[] a, int[] b) {
        int N = a.length;
        if (N < 1 || N != b.length) {
            return;
        }

        int i = 0, j = 0;
        while (i < N && j < N){
            if (a[i] < b[j]){
                i++;
            } else if (a[i] > b[j]){
                j++;
            } else {
                System.out.println(a[i]);
                // 如果下一个元素与当前元素相同，跳过
                while(i+1 < N && a[i] == a[i+1]){
                    i++;
                }
                while(j+1 < N && b[j] == b[j+1]){
                    j++;
                }
                i++;
                j++;
            }
        }
    }

    public static void main(String[] args) {
        int[] a = { 1, 2, 2, 2, 3, 4, 5, 6 };
        int[] b = { 1, 2, 3, 6, 6, 6, 7, 8 };
        printCommon(a, b);
    }
}

我对两个版本的算法评价: 我的更直观, GPT的方法, 扩展性更强.

对于没有接触过 “双指针” 方法的人, 我的解题方法, 可能会更直观, 更便于理解. 虽然代码略有些冗余, 但是交叉遍历的思路, 应该是极容易想到的.
GPT 的算法, 不仅是更直观. 和我的方法, 本质上的 “抽象” 内容也是不一样的.
我的方法, 其实是把两个数组, 当作两个独立的个体, 独立去遍历; 但是 GPT 的双指针法, 本质上, 把两个数组看作一个整体, 在单次循环中, 基于情况, 去调整某个数组对应的指针.
GPT 的算法抽象, 更便于简化类似问题的处理方法.如: 找出三个数组的共同元素.如果对 “双指针” 法有了解, 知道将将所有数组看作一个整体, 把不同数组的遍历, 转换为对数组指针的同时操作, 会很自然地想到 “三指针法”.

更进一步: 我做了一个找到三个数组共同元素的 “三指针” 解法.

编写一个程序，有序打印给定的三个有序数组(含有N个int值)中的所有公共元素，程序在最坏情况下所需的运行时间应该和N成比。

package algs4;

public class Answer1412GptExtend {
    public static void printCommon(int[] a, int[] b, int[] c) {
        int N = a.length;
        if (N < 1 || N != b.length || N != c.length) {
            return;
        }

        int i = 0, j = 0, k = 0;
        while (i < N && j < N) {
            if (a[i] < b[j] || a[i] < c[k]) {
                i++;
            } else if (b[j] < a[i] || b[j] < c[k]) {
                j++;
            } else if (c[k] < b[j] || c[k] < a[i]) {
                k++;
            } else {
                System.out.println(a[i]);
                // 如果下一个元素与当前元素相同，跳过
                while (i + 1 < N && a[i] == a[i + 1]) {
                    i++;
                }
                while (j + 1 < N && b[j] == b[j + 1]) {
                    j++;
                }
                while (k + 1 < N && c[k] == c[k + 1]) {
                    k++;
                }
                i++;
                j++;
                k++;
            }
        }
    }

    public static void main(String[] args) {
        int[] a = { 1, 2, 2, 2, 3, 4, 5, 6 };
        int[] b = { 1, 2, 3, 6, 6, 6, 7, 8 };
        int[] c = { 0, 2, 3, 6, 6, 6, 7, 9 };

        printCommon(a, b, c);
    }
}

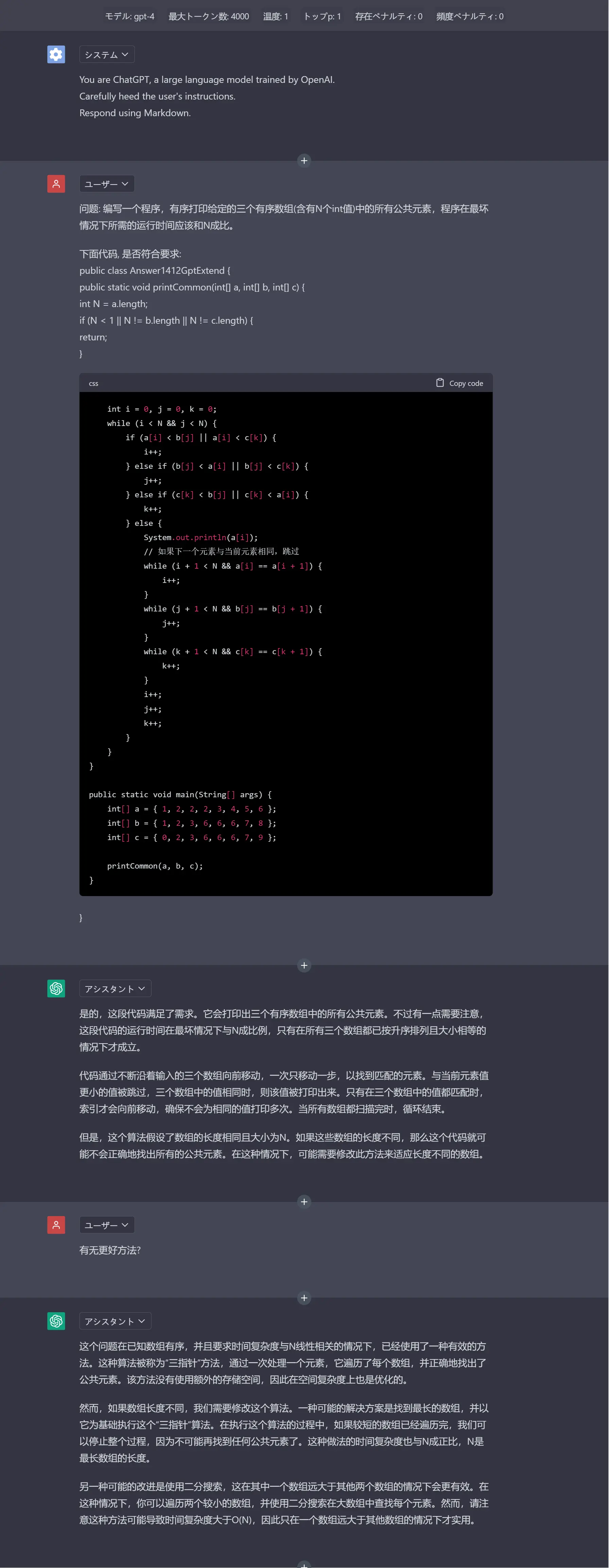
GPT 对话附图:

注意: gpt token 太贵.我 reset 了部分对话. 所以看到的GPT的代码输出, 可能和上文描述的不完全一致.无论如何, 重要问题, 适当多角度问问, 可能会有不同的意外收获.

1412

1412_more