1.4.6 给出以下代码段的运行时间的增长数量级(作为N的函数):

  • a 
    int sum=0;
 for (int n=N;n>0;n/=2)
    for(int i=0;i<n;i++)
        sum++;
  • b 
    int sum=0;
 for (int i=1;i<N;i*=2;
     for(int j=0;j<i;j++)
        sum++;
  • c 
    int sum=0;
 for (int i=1;i<N;i*=2)
    for( int j=0;j<N;j++)
       sum++;

现在看, 这个题目对于算法复杂度的考察, 非常的简单明了, 作为算法复杂度的入门级考察, 非常有价值. 未来, 如果我再度成为面试官时, 一定要用下这道题.

我对算法复杂度的计算, 有点畏惧.所以初始接触时,就给了一个最基本的答案: abc全部是 N². 我的理由是: 一层循环一个N,两层循环就是两个 N*N.

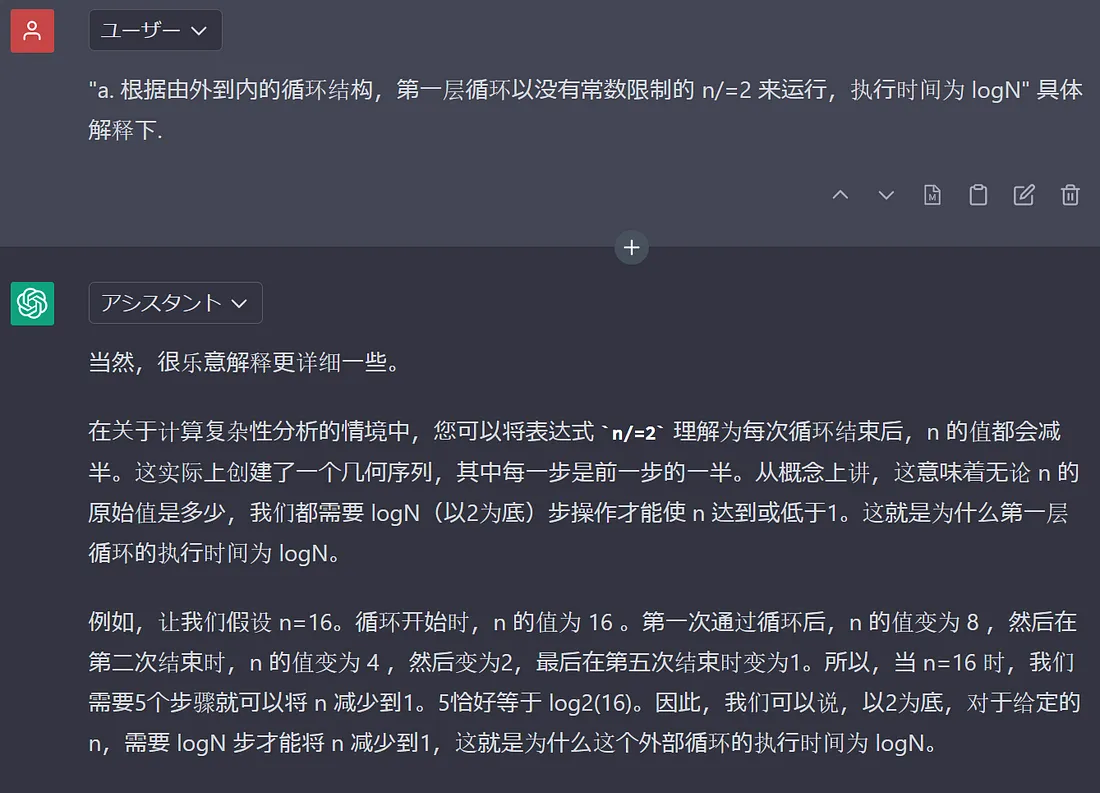
当然, 我的答案是不对的. 但是这个题目,网上进一步深入讨论的少.我几乎没法找到解题资料. 于是就抱着试一试的态度, 试了下 ChatGPT4:

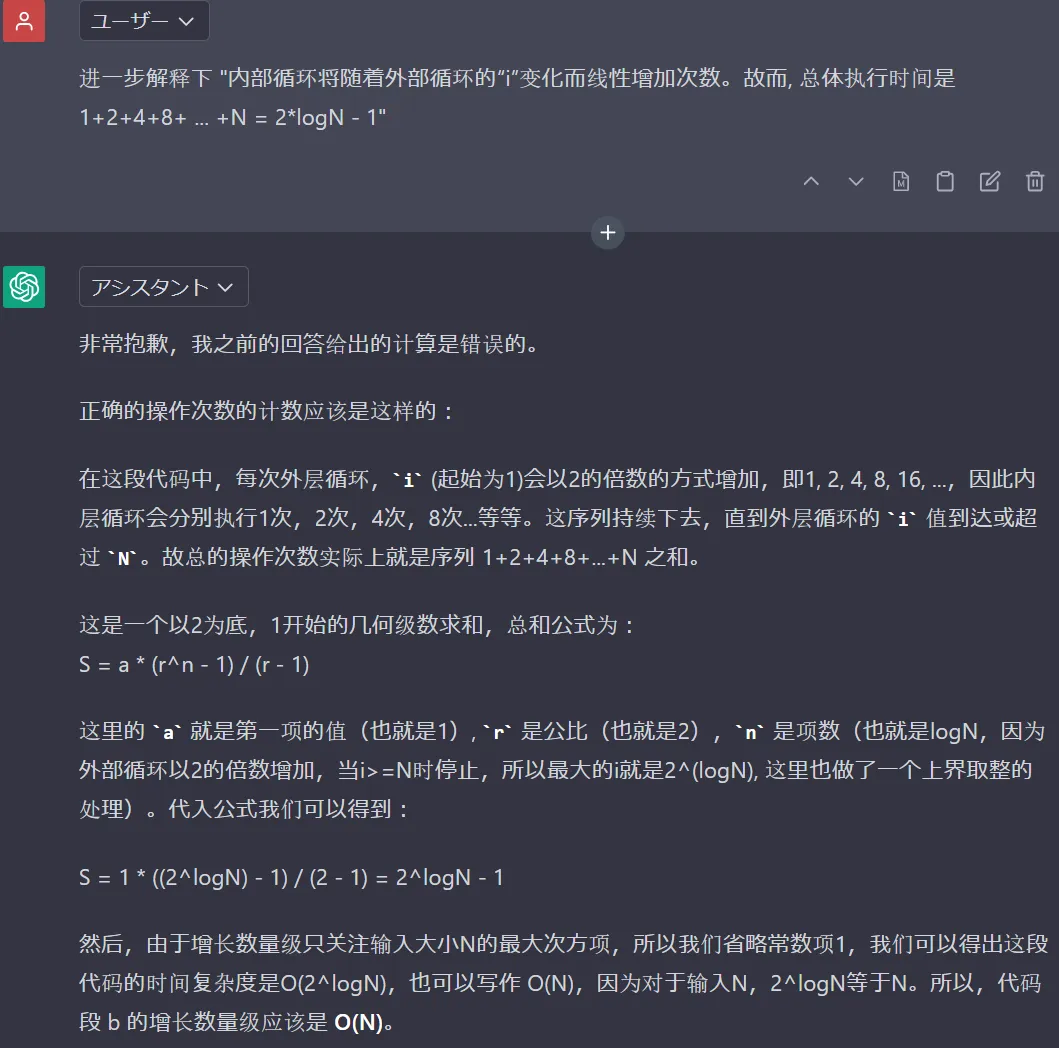
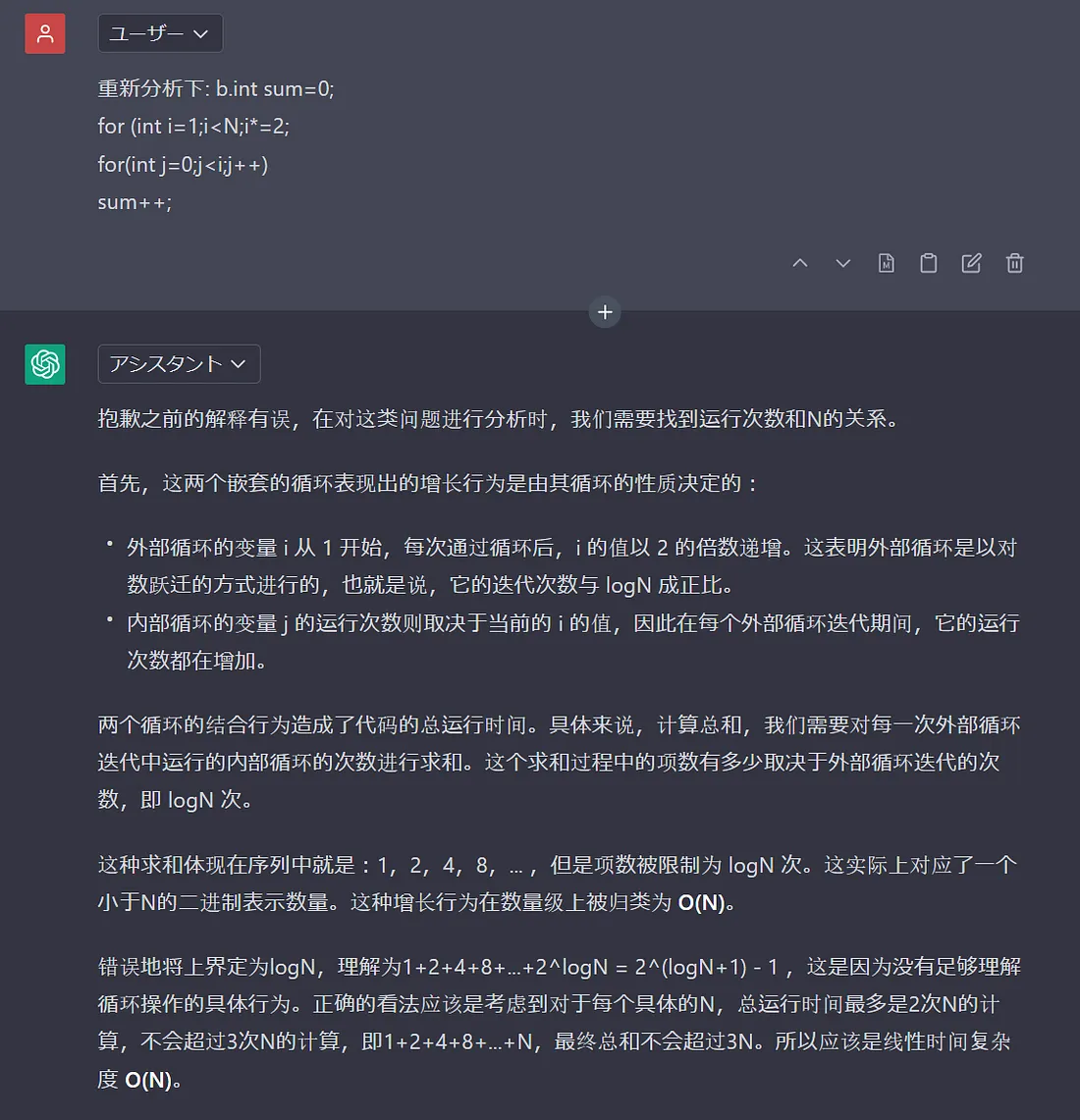
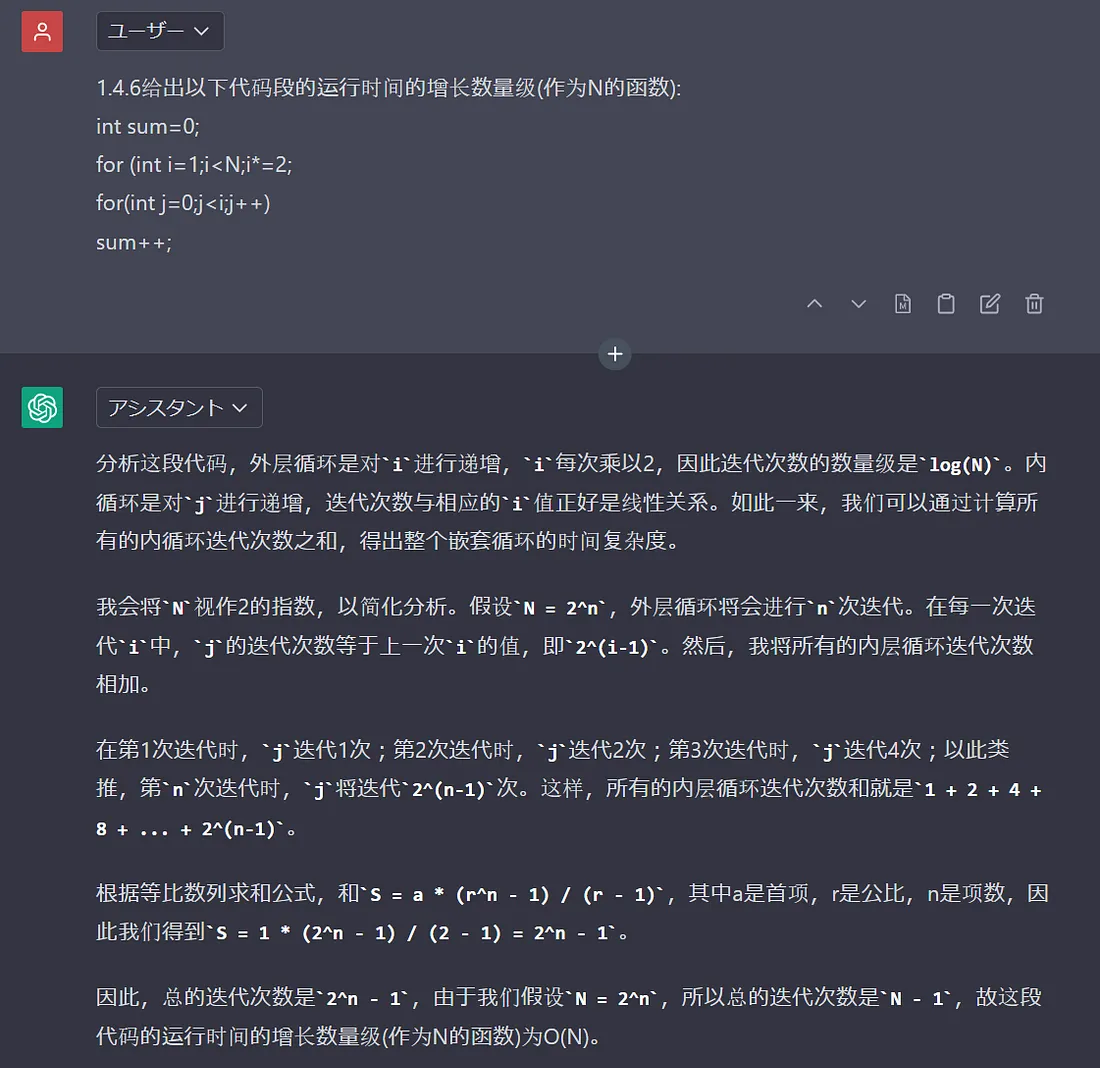
ChatGPT4

ChatGPT4

ChatGPT4

ChatGPT4

ChatGPT4

ChatGPT4

顺便贴下 Google Bard 的三个草稿作为对比:

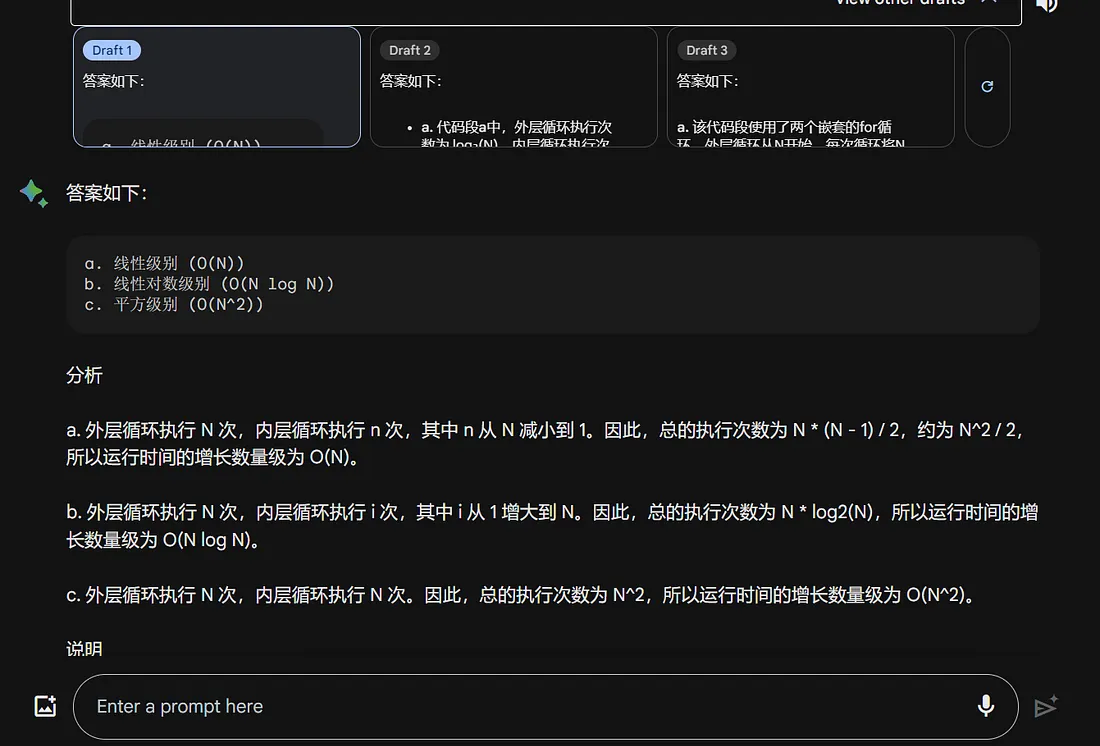
Google Bard

Google Bard

Google Bard

显而易见, a 和 c 的增长数量级是 O(n log n).这一点相对确认. 有分歧的是出现问题b上. 我又单独询问了下 ChatGPT. 结合最后的答复, 我认为 b 的增长数量级应该是 O(n).

循环问题, 本质上都可以用内层循环总的执行次数来计算整体时间复杂度. 在a和c场景下, 内层循环执行次数和外层没有直接关系, 所以直接内外层执行次数相乘, 即可估算总的内层循环执行次数. 而对于b, 内层循环是受制于外层循环的, 此时又可以直接计算出内层循环的执行次数的总和, 所以直接内层循环之和即可. 而内层循环总字数, 本质上就是 等比数列求和. 基于书上给出的 “表1.4.6算法分析常用的近似函数”可知: 1+2+4+8+…+N=2N-1 ~ 2N.所以b的增长数量级应该是 O(n).

从AI的回答来看, bard 可以直接排除了. 在过往的技术类问题的问答中, bard 的表现,确实很一般, 大都存在谬误.

ChatGPT的回答, 也只能说 “仅供参考”.需要一定的专业知识,进一步鉴别. 不过通过针对特定细节的补充询问, 目前看是能得到相对正确的答案,或者给与一定的思路启发的.

问题本身, 也对我很大启发:

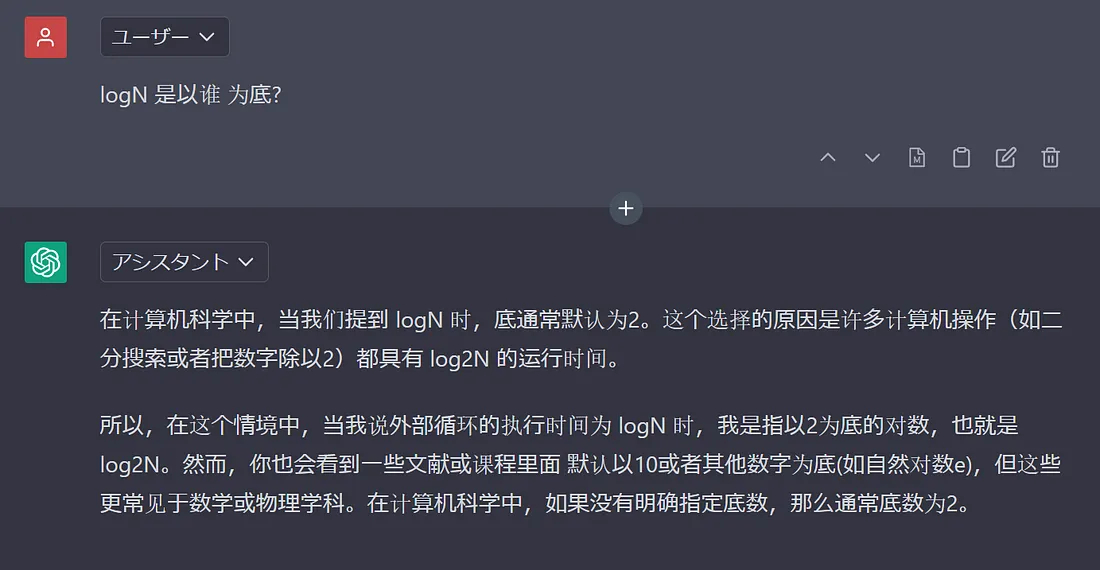
  • *2或者 / 2, 执行次数是: lgN.表示: 以2为底, N的对数. ==> 不是简单的一层循环,就乘以一个N.

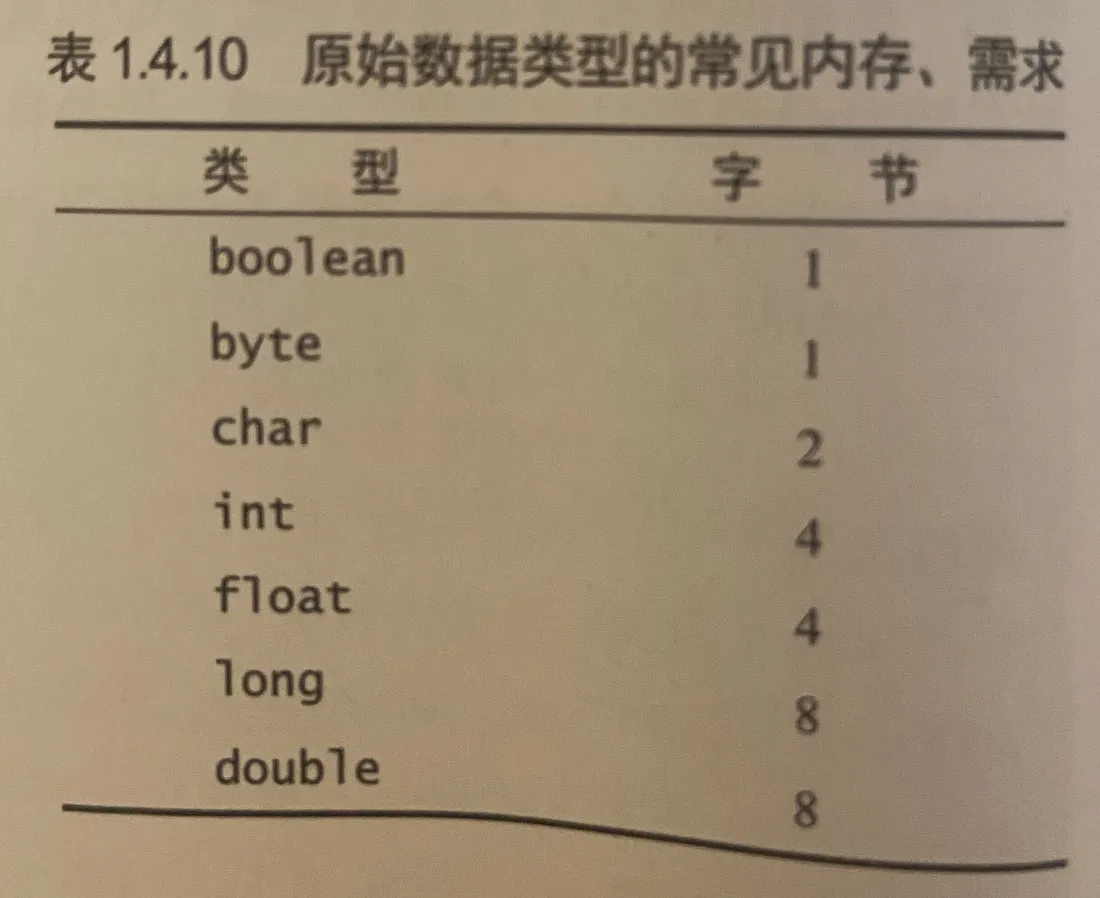
  • 书中给出的几个表格, 很重要. 值得珍藏, 时时翻阅,参考. 应该是足够覆盖常用的复杂度计算场景的.

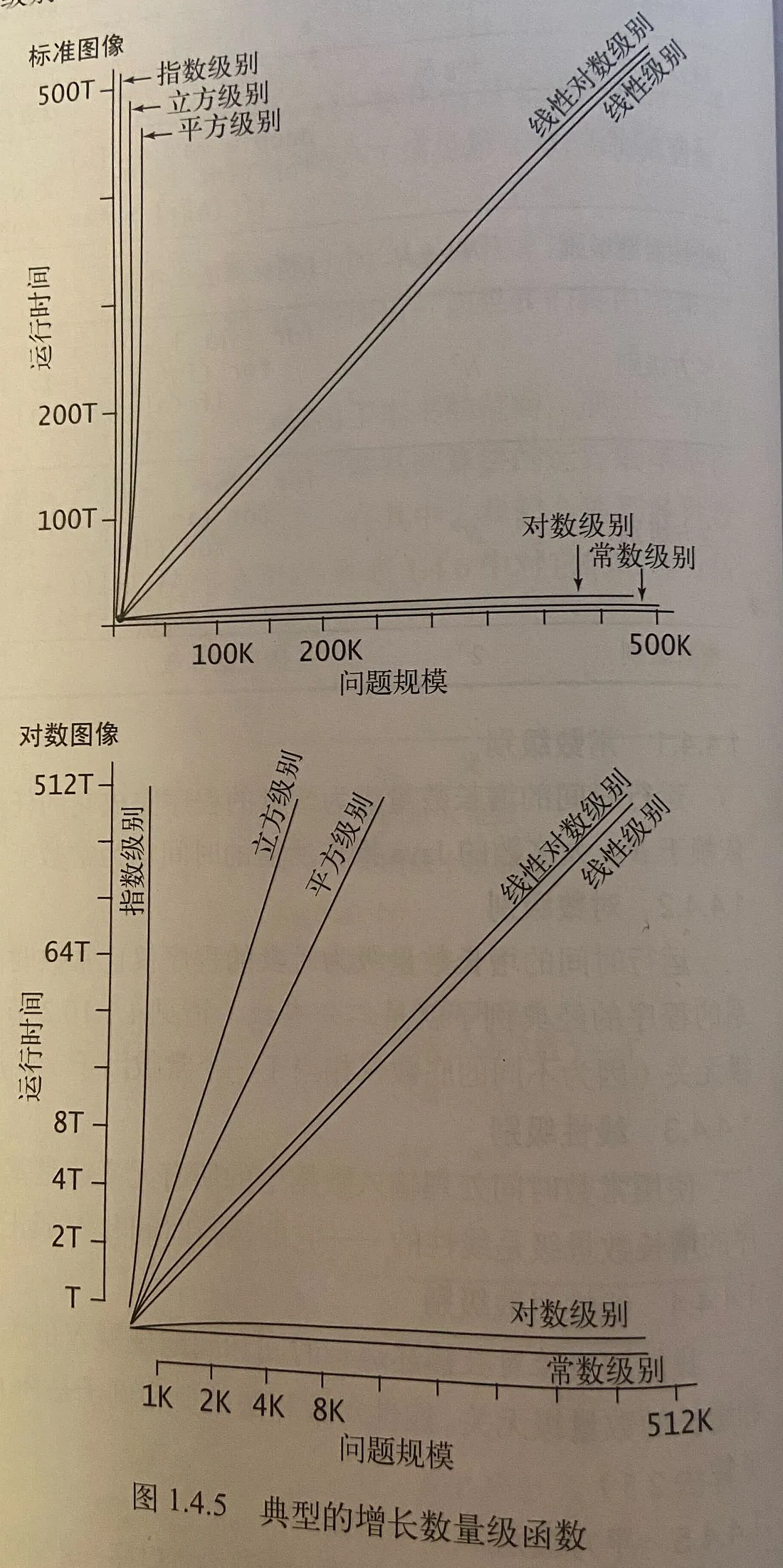
  • 对算法复杂度计算的重要性, 有了进一步的认知. 因为O(n log n), O(n) 和 O(n²) 分别对应 线性对数级别,线性级别,平方级别的运行时间. 三者的运行时间区间,差距是非常大的. ==> 如果我不能从代码层面,准确估算出算法复杂度, 未来可能就不得不加一堆日志来反推算法的性能瓶颈点.

附图, 算法4 书中几个算法分析可能有用的参考图:

algs4

algs4

algs4

algs4

algs4

algs4