algs4–1.4.5 和AI一起讨论做题

我简单做了后, 和 GPT 讨论了下. 因为其他网上可参考的解答, 几乎没有.
我的答案是:
a. N
b. 1
c. 1
d. N^3
e. 1
f.lgN
g.1
GPT 的出版答案是:
a. N + 1 ~ N
b. 1 + 1/N ~ 1
c. (1 + 1/N) * (1 + 2/N) ~ 1
d. 2N^3 - 15N^2 + N ~ 2N^3
e. lg(2N) / lgN ~ 1 (because log(2N) is simply log2 + logN, and log2 is a constant)
f. lg(N^2 + 1) / lgN ~ 2
g. For large values of N, N^100 increases far faster than 2^N. Thus, N^100 / 2^N ~ N^100
问题d, 我和GPT不一样,但是并不影响最后复杂度的估算.
问题f,我的答案是错误的. 因为自己对 对数的运算法则不熟悉. 知识点: lg(N^x) = x * lg(N).
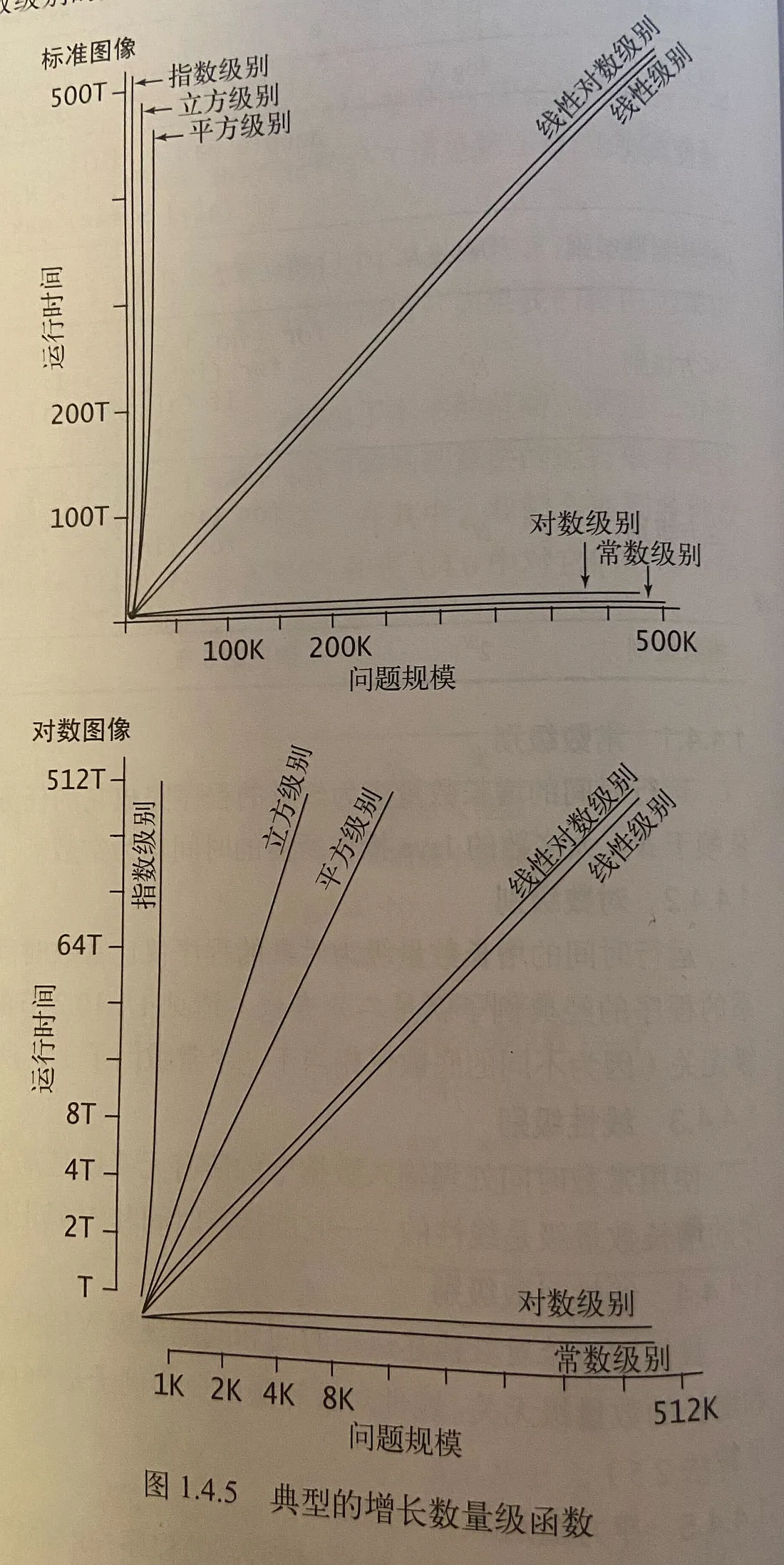
问题g, 是有争议的. GPT 的答案和我看到的图中配图有冲突. 按照图中所示, 指数级别,应该是增长最快的.
又进一步单独询问了下, 比如: “如果把 g 改为: N³ / 2^N 呢?” 此时 GPT 开始给出截然不同的答案, 并且认为:
无论你将多项式的次数提高到多少,总的来说,当 N 趋于无穷大时,指数函数(比如 2^N)的增长速度都要快于多项式函数(比如 N¹⁰)。
这是因为,当 N 足够大时,指数函数的复利增长(每一次都乘以一个固定的数,如 2)将超过多项式函数的简单增长(每一次增加 N 的某个次方)。因此,无论 N 有多大,2^N 都将会比 N¹⁰ 大得多。 所以,我们可以说,对于足够大的 N,N¹⁰ / 2^N ~ 0。
所以, 关于g, 正确的答案,就应该是 0. 而至于我给出的1, 有点无厘头了…
另外, 顺便还单独把g问了下 Bard, Bard 的答案,这次略胜一筹, 甚至还给出了 N^m 和 2^N 哪个更大的临界条件:
具体来说,当 N≥100 时,N100/2N≈0;当 N<100 时,N100/2N≈N100/2N。
不过…意义不大, 此时更应该着重考虑 N 足够大时的场景.
截止目前, AI 并没有一次性给出所有问题的正确或者合理的答案. 我对那些缺乏基础的编程技能, 却又试图借助 AI 编程, 写一个自己产品的人, 真的有点不看好. 他们写的程序,或许能跑起来, 但是真的会是正确的吗?在关键业务上, 某个不易察觉的错误, 可能会引起无法承受的损失呢…