algs4 1.3.49究竟需要多少个Stack?

1.3.49栈与队列。用有限个栈实现一个队列，保证每个队列操作(在最坏的情况下)都只需要常数次的栈操作。警告:非常难！

这个问题, 我研究了1天了. 我认为,需要7个, 而不是6个.

问题本身是非常有现实意义的.它传递的思想是: 尽可能将操作成本分摊到每一次操作; 这样可以不让某一次操作,产生大的时间消耗. 有点抽象. 可以类比下网络波动. 题目本身,是希望网络速度能尽量平稳, 同时能保持相对较高的速度; 而不是时不时地网络剧烈抖动.

即使在现实世界, 这种思想,也是非常有价值的. 将一个耗时的任务, 适当拆解, 然后和其他时间段内的任务,适当绑定. 这样, 虽然一整天, 过得都会略有压力, 但是可以保证重要任务, 始终能平稳可靠地推进.

硬件, 有极限, 某种剧烈波动, 可能会直接导致硬件瓦解/崩溃 — 让我想起了,小时候时不时就烧保险丝导致停电的日子… 人的意志力,所能承受的压力, 也必然是有极限的. 连续处于压力10 的状态, 可能会让人有些许不自在, 但是总是能克服的; 但是如果大部分时间处于压力1, 然后在某个时间段瞬间来到压力100 的状态, 大概率会因为压力过大,直接终止任务.

我的日语学习, 中止有2个星期了. 回国了一趟, 处理家事, 时间确实仓促确实是直接原因. 但是, 我现在一想到,一旦开始学习, 就要投入2~4小时, 心里就发毛… 连续几个小时,啥也不干,就一直学….想想就觉得恐怖. 显而易见, 这个时间成本, 超过了我当前心里压力的上限了. 我要适度拆解下…. 今天会适着将日语学习,拆分到起床,吃饭前后等日常事务中去.每次最好不超过10分钟.

回到问题本身, 为什么一定需要7个Stack?或者说具体需要哪7个Stack?

    private Stack<Item> T = new Stack<>(); // 队列尾部,用于 enqueue 入队操作.
    private Stack<Item> H = new Stack<>(); // 队列头部, 用于 dequeue 出队操作.

    private Stack<Item> TS = new Stack<>(); // 暂存 T 中的数据.
    private Stack<Item> TR = new Stack<>(); // T 反转后的数据,后续会拼接 HR 中的元素.
    private Stack<Item> TRC = new Stack<>(); // TR 的副本, 与T中元素完全一致.
    private Stack<Item> HR = new Stack<>(); // H 反转后的数据.
    private Stack<Item> HC = new Stack<>(); // H 的副本, 初始与H中的元素完全一致.

基于代码,我具体阐述下:

T和H,显而易见,是必须的.
TR和HR是反转后的Stack, 也是必须的.因为不反转Stack,就无法二次拼接.
TS 和 HC 用于保证: 在反转Stack时, 能可靠地进行队列的入队和出队.
TRC, 看起来是有争议的. 但是如果仅基于栈的操作来解答题目,则必须有TRC,进而基于TRC得到 HC.即: H 的副本,并不是从H来的, 而是和H同步产生的.

我看了网上的两篇文章.总觉得有些晦涩难懂. 在我看明白之后, 发现他们思路大致类似,但是在描述各个关键节点时, 没有合适地 “抽象”, 导致引起了某种理解和阅读上的混乱. 这从他们的最终编码实现上, 也能很清晰地感受到.

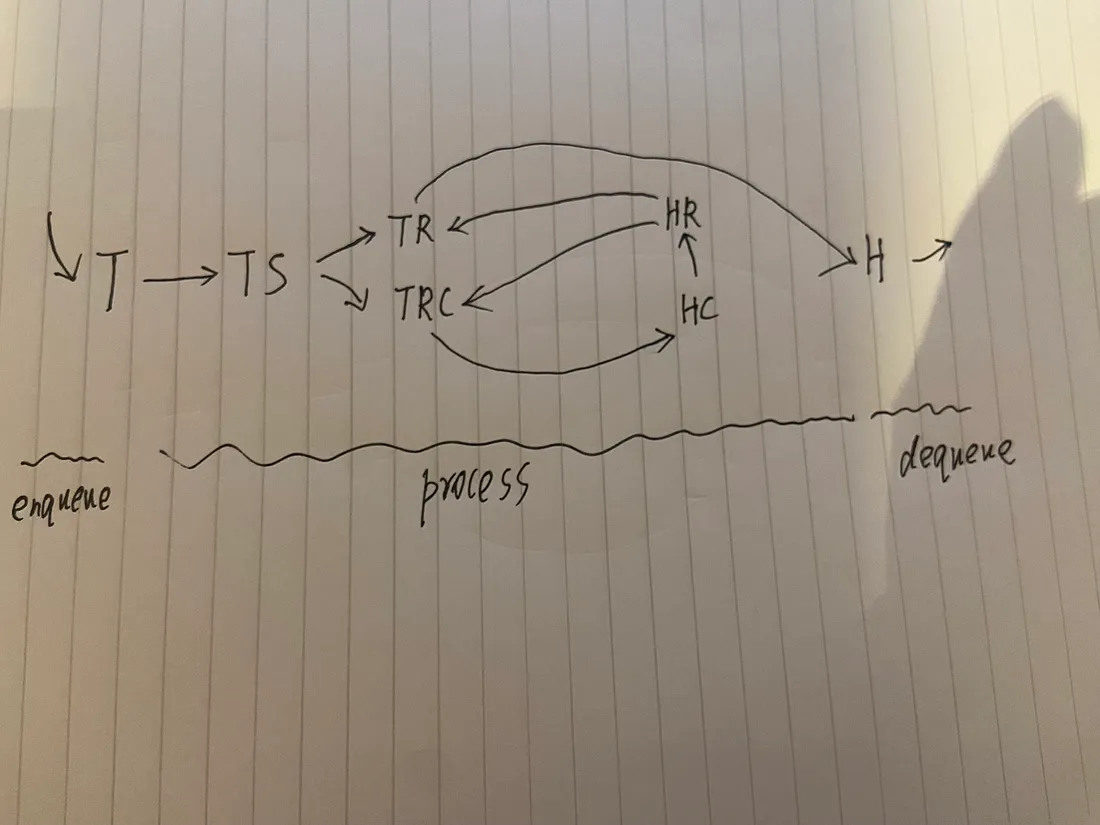
Data Flow

我的设计目标非常清晰:

enqueue方法, 将仅需要关心 T; dequeue方法, 将仅需要关心 H.
中间的各种 Stack反转操作, 将封装为一个统一的 process方法.
enqueue 和 dequeue 方法内部统一调用一次process 方法. 理清思路和设计目标后,代码本身, 没啥难度:

package study.algorithm;

import edu.princeton.cs.algs4.StdOut;

public class QueueFromSevenStack<Item> {
    private boolean isRevert = false; // 是否在反转 Stack.
    private boolean isConcat = false; // 是否在拼接 Stack.

    private Stack<Item> T = new Stack<>(); // 队列尾部,用于 enqueue 入队操作.
    private Stack<Item> H = new Stack<>(); // 队列头部, 用于 dequeue 出队操作.

    private Stack<Item> TS = new Stack<>(); // 暂存 T 中的数据.
    private Stack<Item> TR = new Stack<>(); // T 反转后的数据,后续会拼接 HR 中的元素.
    private Stack<Item> TRC = new Stack<>(); // TR 的副本, 与T中元素完全一致.
    private Stack<Item> HR = new Stack<>(); // H 反转后的数据.
    private Stack<Item> HC = new Stack<>(); // H 的副本, 初始与H中的元素完全一致.

    private Integer dequeueItemCount = 0; // 在 反转或拼接Stack过程中, 出队的元素数量.

    public void enqueue(Item item) {
        T.push(item);

        process(true);
    }

    public Item dequeue() {
        if(H.isEmpty()){
            return null;
        }

        Item item = H.pop();

        process(false);

        return item;
    }

    private void process(Boolean isEnqueue) {
        if(!isEnqueue){ 
            if(isRevert || isConcat){
                dequeueItemCount += 1;
            } else {
                // 一种特殊情况: 仅存在 dequeue 操作时,直接 pop H的副本, 不用额外计数.
                HC.pop();
            }
        }

        if (!isRevert && !isConcat && !T.isEmpty() && T.size() >= H.size()) {
            // 仅在必要时进入 Revert Stack阶段.
            TS = T;
            T = new Stack<>();
            isRevert = true;
        }

        if (isRevert) {
            if (!TS.isEmpty()) {
                Item item = TS.pop();
                TR.push(item);
                TRC.push(item);
            }

            if (!HC.isEmpty()) {
                Item item = HC.pop();
                HR.push(item);
            }
        }

        if (TS.isEmpty() && HC.isEmpty()) {
            isRevert = false;
            isConcat = true;
        }

        if (isConcat) {
            if (!HR.isEmpty() && HR.size() > dequeueItemCount) {
                Item item = HR.pop();
                TR.push(item);
                TRC.push(item);
            }

            if (HR.isEmpty() || HR.size() == dequeueItemCount) {
                H = TR;
                HC = TRC;

                TR = new Stack<>();
                TRC = new Stack<>();
                HR = new Stack<>();

                isConcat = false;
                dequeueItemCount = 0;
            }
        }
    }

    public static void main(String[] args) {
        QueueFromSevenStack<Integer> q = new QueueFromSevenStack<>();
        StdOut.println("enqueue 0");
        q.enqueue(0);
        StdOut.println("dequeue: " + q.dequeue());
        StdOut.println("enqueue 1");
        q.enqueue(1);
        StdOut.println("enqueue 2~3");
        q.enqueue(2);
        q.enqueue(3);
        StdOut.println("dequeue: " + q.dequeue());
        StdOut.println("enqueue 4 ~ 6");
        q.enqueue(4);
        q.enqueue(5);
        q.enqueue(6);
        StdOut.println("dequeue: " + q.dequeue());
        StdOut.println("dequeue: " + q.dequeue());
        StdOut.println("enqueue 7 ~ 10");
        q.enqueue(7);
        q.enqueue(8);
        q.enqueue(9);
        q.enqueue(10);

        StdOut.println("dequeue: " + q.dequeue());
        StdOut.println("dequeue: " + q.dequeue());
        StdOut.println("dequeue: " + q.dequeue());
        StdOut.println("dequeue: " + q.dequeue());
        StdOut.println("dequeue: " + q.dequeue());
        StdOut.println("dequeue: " + q.dequeue());
        StdOut.println("dequeue: " + q.dequeue());
    }
}

参考文章: