算法4 1.4.2 如何正确处理 int值溢出的情况?
1.4.2 修改ThreeSum,正确处理两个较大的 int 值相加可能溢出的情况.
基于我通常的学习方法论: 独立思考的过程要比得到”正确”的答案,更重要. 我先尝试着自己处理了下.
初始思路, 确实更多的是考虑 “避免溢出”.于是加了很多 if else的判断,来保证两个值相加不会溢出.后来发现, 我写的判定会漏掉一些特殊情况,如: { Integer.MAX_VALUE, 1, Integer.MIN_VALUE }
后来稍微整理了下思路.尝试先搞清楚: int值溢出时,到底会发生什么? 进而决定,是否真的有必要避免值溢出,才能正确处理问题?
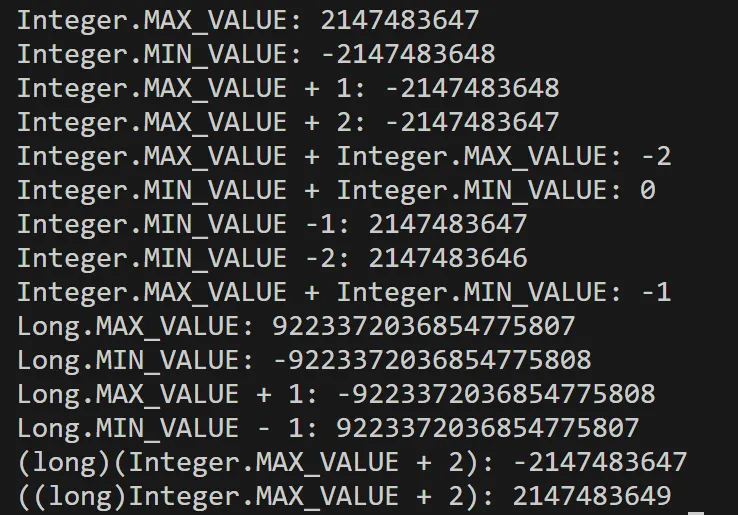
/*
* Integer.MAX_VALUE: 2147483647
* Integer.MIN_VALUE: -2147483648
* Integer.MAX_VALUE + 1: -2147483648
* Integer.MAX_VALUE + 2: -2147483647
* Integer.MAX_VALUE + Integer.MAX_VALUE: -2
* Integer.MIN_VALUE + Integer.MIN_VALUE: 0
* Integer.MIN_VALUE -1: 2147483647
* Integer.MIN_VALUE -2: 2147483646
* Integer.MAX_VALUE + Integer.MIN_VALUE: -1
*/
显而易见:
- 正向溢出时, 会得到一个负数. 基于问题本身,这最多会导致: 三个正数 int 的和可能是0.
- 负向溢出时, 会得到一个负数.基于问题本身, 这最多会导致: 三个负数int的和可能是0.
- 两个正数相加溢出, 如果第三个数也是负数, 那此时三个数的和一定是负数, 而不是要找的 “零”, 所以不用特殊考虑.负向溢出,同理.
也就是说: int值溢出的情况, 对 ThreeSum 算法的影响,极其有限.对应的场景, 可以很轻易地排除掉. 只有三个正数或者三个负数的场景, 才有可能触发这个问题,但是 三个正数或者三个负数的和一定不是零.
最终,我的解决方法,也非常简单, 在里面加一层额外的判断即可:
public static int count(int[] a) {
int N = a.length;
int cnt = 0;
for (int i = 0; i < N; i++) {
for (int j = i + 1; j < N; j++) {
for (int k = j + 1; k < N; k++) {
// 新加的判断.
if ((a[i] > 0 && a[j] > 0 && a[k] > 0) ||
(a[i] < 0 && a[j] < 0 && a[k] < 0)) {
continue;
}
if (a[i] + a[j] + a[k] == 0) {
cnt++;
}
}
}
}
return cnt;
}
问题本身, 还设计了一个简单的case来检证:
public static void main(String[] args) {
int[] a = { Integer.MAX_VALUE, 2, 2147483647, Integer.MIN_VALUE, -1, -2147483647 };
int cnt = count(a);
// 修改前: cnt 是2; 修改后 cnt是0.
StdOut.println("count: " + cnt);
}
我自己的解答, 到此算是告一段落.
问题本身, 费了些周折, 上网看下其他人的解法. 他们大都是采用的另一种思路: 避免溢出. 不过避免溢出的方法更简洁些: 显式或隐式地 将变量声明为 long 类型. 思路,值得借鉴; 但是在真实场景中, 如果是很重要的场景, 大概率不会用这种方式. 因为 long 类型也是有可能溢出的. 即使换成 BigInteger 也是有可能溢出的. 不去分析 溢出本身,对问题的具体影响, 简单粗暴地屏蔽 “溢出”, 多少让人心里隐隐有些不安. 这样的代码, 不加特殊的备注, 以后可能大概率会是一个隐患.
必须说明的是: 不同的语言实现, 这个算法的 int值溢出情况的处理方法,可能是不同的. 因为不同语言种, 关于如何 “溢出”, 实现可能是不一样的. 比如python3, 理论上不需要处理 int 溢出的情况了. 而如果一门语言, 是用 Crash 的方式,来表达 值溢出, 可能就必须换用 long 类型了.